這幾天Pelosi規劃訪台成為世界矚目的大事。在訪台之前，許多分析都以「賽局」兩字作為噱頭，最終開獎有勝有負。但是賽局理論（Game Theory）本身對於相關的分析方式是有嚴謹的定義的。假如真的要使用賽局理論分析Pelosi訪台，會是什麼樣的分析呢？
美國眾議院議長裴洛西（Nancy Pelosi）。圖片來源：美聯社／達志影像首先，賽局理論一開始就需要有固定的玩家（player）、策略（strategy）、以及對每一種結局的偏好（utility）。以這一次的Pelosi訪台為例，假如用最簡單的賽局版本，那美國是一個賽局內的玩家，有兩種策略，分別為Pelosi訪台（V）或者不訪台（N）。
而賽局內另一個玩家是中國。中國同樣有兩種策略，一種是懲罰美國與台灣（A）、而第二個策略是假裝沒看到（X）。因此，兩個玩家互動下就可能有四種不同的結果：
在決定完策略之後，接著就是玩家對所有可能的結果進行偏好排序，來找出可能的納許均衡解（ Nash Equilibrium）。然而，這裡我們可以看到兩種可能性，因為這裡有資訊不完整的情況。其中，中國到底國力是強是弱？是否真的會打？這裡是資訊不透明之下只有中國自己知道的。因此，對於美國來說，美國就需要猜測中國的可能狀態（type），不同的狀態就會導致中國跟美國的偏好不同。
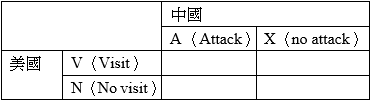
舉例來說，假如中國是真的強大、雖遠必誅，美國的拜訪會讓中國不惜一戰兩敗俱傷。那在此時，美國的偏好可能為 VX > NX > NA > VA。VX為美國拜訪但是中國不打，是美國最希望發生的；FA是美國拜訪然後強大的中國反擊、兩敗俱傷，是美國的最不喜歡的偏好；而中間兩個NX與NA，考量到美國假如被中國威脅而不敢打（NA），則有失名譽，比本來毫無事情發生（NX）還差。因此最後排名如上。
同樣地，假如中國真的強大，那中國的偏好可能為NA>NX>VA>VX。最佳解是用武力威脅成功勸退美國（NA）、最差解是美國訪問而自己按兵不動（VX），中間兩個選項則是雙方都維持現狀比兩敗俱傷好（NX>VA）。
當把上述兩排偏好放進賽局裡面，如下表。在下表之中，A是中國的最上策（Dominant Strategy），無論美國訪不訪問都要擺出架式。最後根據納許的方法，可以得到這個賽局的均衡解為（N,A）=（2,4），中國武力恫嚇、美國則羞辱的不訪問（表格中加黑與底線）。
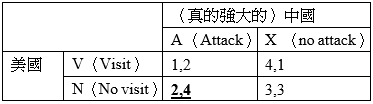
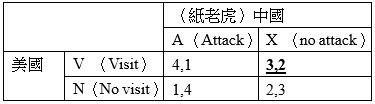
然而，另外一種可能的中國，是假裝強大的中國。假如中國只是紙老虎，那麼美國的偏好為VA>VX>NX>NA。最好是訪問台灣並戳破中國的假面（VA）、略大於訪問台灣但中國不表態 （VX）。假如中國只是紙老虎，那麼不去訪問台灣就虧大了（NA）、比中國不表態但還不去還遭（NX）。
就在同時，對於是紙老虎型態的中國來說，其偏好順序為NA>NX>VX>VA。最好的情況是用紙老虎嚇唬到美國不敢訪問（NA）、最糟則是嚇唬後美國照訪不誤（VA）、中間則是美國不訪問比訪問好（NX>VX）。
我們同樣可以把兩者的偏好寫進賽局表中，如下表。在這個表中，納許均衡解為VX，也就是中國保持沉默（而不會被戳破紙老虎面具），而美國順利訪問。
舉例來說，假如中國是真的強大、雖遠必誅，美國的拜訪會讓中國不惜一戰兩敗俱傷。那在此時，美國的偏好可能為 VX > NX > NA > VA。VX為美國拜訪但是中國不打，是美國最希望發生的；FA是美國拜訪然後強大的中國反擊、兩敗俱傷，是美國的最不喜歡的偏好；而中間兩個NX與NA，考量到美國假如被中國威脅而不敢打（NA），則有失名譽，比本來毫無事情發生（NX）還糟。因此最後排名如上。
這個賽局最有趣的狀態，是因為中國的資訊不透明，所以美國可能一開始並不知道中國是哪一種型態，而中國知道自己的型態。基於中國可能的不同型態，美國可能需要有對應的策略。假如我們把兩個賽局結合，並納入中國的不確定性，那完整的賽局可能如下：
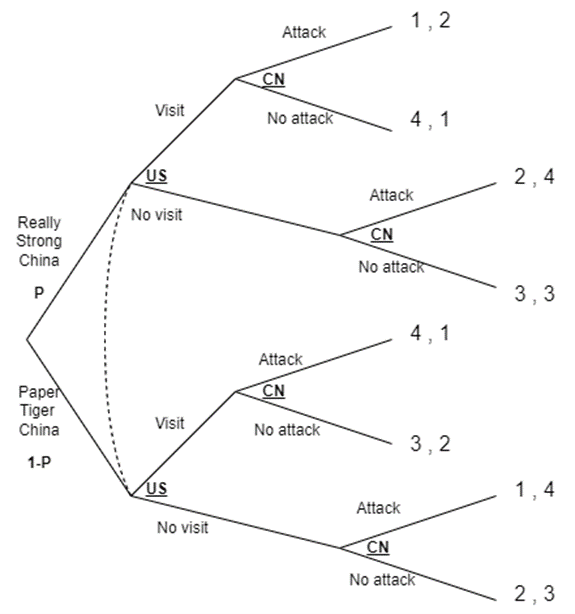完整的賽局。圖片來源：作者提供在這個賽局之中，美國一開始不確定中國是否真的強大，因此美國假設中國強大的機率為P、中國為紙老虎的機率為1-P。在美國決策之後，中國因為已經知道自己的型態，因此可以照美國的決策來決定自己要用什麼策略。在刪去中國不會選擇的選項後，最後美國假如選擇拜訪Visit，則期望值為P+3（1-P）=3-2P；假如選擇不拜訪No visit，則美國期望值為2P+（1-P）=1+P。在兩權相較之下，假如3-2P>1+P，也就是假如2/3>P，那美國就有動機選擇Visit。
假如用白話文說，就是美國假如評估中國「真的強大」的機率不高（2/3>P）時，就更可能在資訊不明的情況下仍然選擇訪台；相較之下，假如美國認為中國強大的機率很高（P>2/3）時，此時就會選擇不要訪台。假如我們事後諸葛，從美國最後選擇訪台來推估，那麼很可能是美國內部經評估後覺得中國真的強大的機率不高，這個推估也可以供台灣參考。
没有评论:
发表评论